Matlab Program For Dolph Chebyshev Array Definition

In section II, application of Chebyshev Polynomial is lobe level (SLL) reduction. Other part of the search space is defined with section VI in which. Introduced by Dolph [3], investigated by others personal best and global best positions respectively. Linear array. Using conventional methods a separate MATLAB code has.

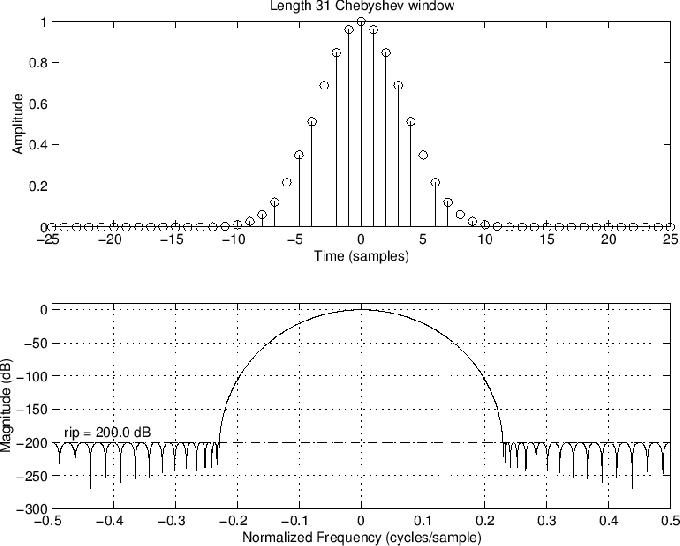
Β = cos [ 1 / N cosh − 1 ( 10 α ) ] α determines the level of the sidelobe attenuation. The level of the sidelobe attenuation is equal to − 20 α. For example, 100 dB of attenuation results from setting α = 5 The discrete-time Dolph-Chebyshev window is obtained by taking the inverse DFT of W ^ ( k ) and scaling the result to have a peak value of 1.

Construction H = sigwin.chebwin returns a Dolph-Chebyshev window object H of length 64 with relative sidelobe attenuation of 100 dB. H = sigwin.chebwin( Length) returns a Dolph-Chebyshev window object H of length Length with relative sidelobe attenuation of 100 dB. Length requires a positive integer. Entering a positive noninteger value for Length rounds the length to the nearest integer. A window length of 1 results in a window with a single value equal to 1.

H = sigwin.chebwin( Length, SidelobeAtten) returns a Dolph-Chebyshev window object with relative sidelobe attenuation of atten_param dB.